Explicit Gradient Differentiation
Explicit Gradient
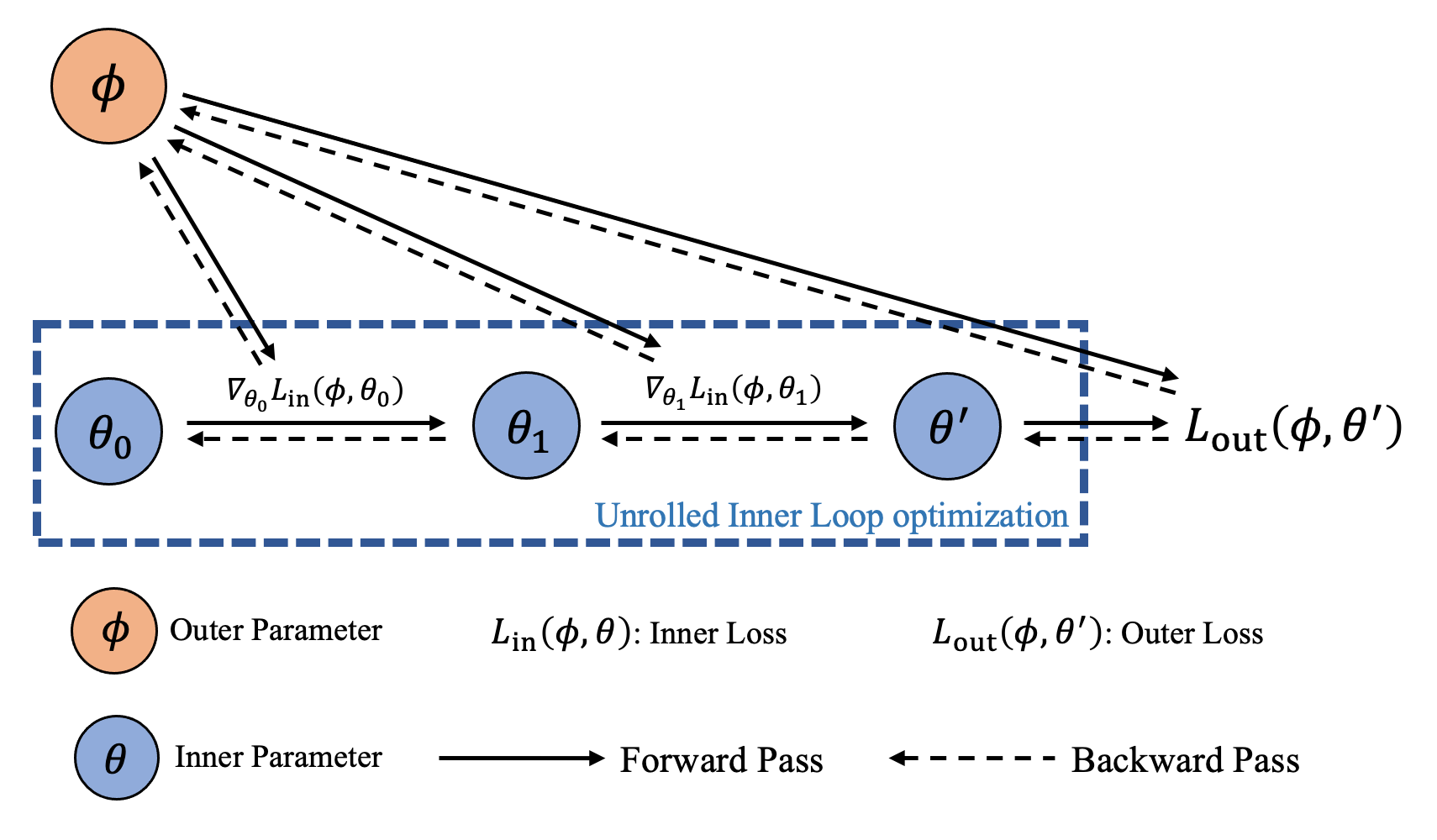
The idea of explicit gradient is to treat the gradient step as a differentiable function and try to backpropagate through the unrolled optimization path. Namely, given
we would like to compute the gradient \(\nabla_{\boldsymbol{\phi}} \boldsymbol{\theta}^{\prime} (\boldsymbol{\phi})\). This is usually done by AutoDiff through an inner optimization’s unrolled iterates.
Differentiable Functional Optimizers
By passing the argument inplace as False to the update functions, we can make the optimization differentiable.
Here is an example of making torchopt.adam() differentiable.
opt = torchopt.adam()
# Define meta and inner parameters
meta_params = ...
fmodel, params = make_functional(model)
# Initialize optimizer state
state = opt.init(params)
for iter in range(iter_times):
loss = inner_loss(fmodel, params, meta_params)
grads = torch.autograd.grad(loss, params)
# Apply non-inplace parameter update
updates, state = opt.update(grads, state, inplace=False)
params = torchopt.apply_updates(params, updates)
loss = outer_loss(fmodel, params, meta_params)
meta_grads = torch.autograd.grad(loss, meta_params)
Differentiable OOP Meta-Optimizers
For PyTorch-like API (e.g., step()), we designed a base class torchopt.MetaOptimizer to wrap our functional optimizers to become differentiable OOP meta-optimizers.
|
The base class for high-level differentiable optimizers. |
|
The differentiable AdaDelta optimizer. |
|
alias of |
|
The differentiable AdaGrad optimizer. |
|
alias of |
|
The differentiable Adam optimizer. |
|
The differentiable AdamW optimizer. |
|
The differentiable AdaMax optimizer. |
|
alias of |
|
The differentiable RAdam optimizer. |
|
The differentiable RMSProp optimizer. |
|
The differentiable Stochastic Gradient Descent optimizer. |
By combining low-level API torchopt.MetaOptimizer with the previous functional optimizer, we can achieve high-level API:
# Low-level API
optim = torchopt.MetaOptimizer(net, torchopt.sgd(lr=1.0))
# High-level API
optim = torchopt.MetaSGD(net, lr=1.0)
Here is an example of using the OOP API torchopt.MetaAdam to conduct meta-gradient calculation.
# Define meta and inner parameters
meta_params = ...
model = ...
# Define differentiable optimizer
opt = torchopt.MetaAdam(model)
for iter in range(iter_times):
# Perform the inner update
loss = inner_loss(model, meta_params)
opt.step(loss)
loss = outer_loss(model, meta_params)
loss.backward()
CPU/GPU Accelerated Optimizer
TorchOpt performs the symbolic reduction by manually writing the forward and backward functions using C++ OpenMP (CPU) and CUDA (GPU), which largely increase meta-gradient computational efficiency.
Users can use accelerated optimizer by setting the use_accelerated_op as True.
TorchOpt will automatically detect the device and allocate the corresponding accelerated optimizer.
# Check whether the `accelerated_op` is available:
torchopt.accelerated_op_available(torch.device('cpu'))
torchopt.accelerated_op_available(torch.device('cuda'))
net = Net(1).cuda()
optim = torchopt.Adam(net.parameters(), lr=1.0, use_accelerated_op=True)
General Utilities
We provide the torchopt.extract_state_dict() and torchopt.recover_state_dict() functions to extract and restore the state of network and optimizer.
By default, the extracted state dictionary is a reference (this design is for accumulating gradient of multi-task batch training, MAML for example).
You can also set by='copy' to extract the copy of the state dictionary or set by='deepcopy' to have a detached copy.
|
Extract target state. |
|
Recover state. |
|
Stop the gradient for the input object. |
Here is an usage example.
net = Net()
x = nn.Parameter(torch.tensor(2.0), requires_grad=True)
optim = torchopt.MetaAdam(net, lr=1.0)
# Get the reference of state dictionary
init_net_state = torchopt.extract_state_dict(net, by='reference')
init_optim_state = torchopt.extract_state_dict(optim, by='reference')
# If set `detach_buffers=True`, the parameters are referenced as references while buffers are detached copies
init_net_state = torchopt.extract_state_dict(net, by='reference', detach_buffers=True)
# Set `copy` to get the copy of the state dictionary
init_net_state_copy = torchopt.extract_state_dict(net, by='copy')
init_optim_state_copy = torchopt.extract_state_dict(optim, by='copy')
# Set `deepcopy` to get the detached copy of state dictionary
init_net_state_deepcopy = torchopt.extract_state_dict(net, by='deepcopy')
init_optim_state_deepcopy = torchopt.extract_state_dict(optim, by='deepcopy')
# Conduct 2 inner-loop optimization
for i in range(2):
inner_loss = net(x)
optim.step(inner_loss)
print(f'a = {net.a!r}')
# Recover and reconduct 2 inner-loop optimization
torchopt.recover_state_dict(net, init_net_state)
torchopt.recover_state_dict(optim, init_optim_state)
for i in range(2):
inner_loss = net(x)
optim.step(inner_loss)
print(f'a = {net.a!r}') # the same result
Notebook Tutorial
Check the notebook tutorials at Meta Optimizer and Stop Gradient.